Archive for the ‘数学’ Category
 0 で割ってはいけないのはなぜ?
0 で割ってはいけないのはなぜ?
少々古い話になってしまいますが、
Togetter 「小学校には9÷0=0というオレルールがあるらしい。」 http://togetter.com/li/412606
という話題がtwitterのタイムラインで流行っていましたね。
これは、小学校の教員が 「9÷0=0」 と教えていて、
それを知った人たちが「おいおい教員が間違ったことを教えるなよ」と異を唱えていたものと記憶しています。
ところで、そもそもどうして「9÷0=0」では誤りなんでしょうか。いざ説明しようとすると正確には答えられない人が多いのではないでしょうか。
それもそのはず、割り算を習うはずの小学校では多くの場合 「0で割ってはいけない(禁止)」 と教えられます。
基本的に小学校で現れる計算問題には0で割るような問題が現れないことが多いと聞きます。
このエントリでは、「0で割ってはいけないこと」 を数学的に証明したいと思います。
ここで気を付けなければならないことは、ここで言う「数学的な証明」とは何か、ということです。
数学的な証明とは、ある「前提」をおいて、この前提によって論理的に導いた「結果」から、
証明したい「主張」の真偽を示すものです。
数学では、この「前提」のことを公理、「結果」のことを帰結、「主張」のことを命題と呼んでいます。
当然、前提とする公理が異なれば、その帰結は異なり、命題の真偽も異なります。
もし、議論していてお互いの言っている結果(帰結)が異なっている場合、前提(公理)が異なることを疑ってみるべきです。
 代数方程式とガロア理論
代数方程式とガロア理論
某勉強会で発表した資料です。せっかく時間をかけてまとめたので、Slide share に投稿しました。
内容は、方程式が解くことができる仕組みを説明した「ガロア理論」についてです。
ガロア理論を使って、五次方程式が解けないことを示すまで、を初学者向けに説明することを試みます。
わかりやすいことに念頭をおいて作ったため、多少の不正確さはあると思いますが、
興味を持った方はぜひ参考書にトライしてみてください。
※2015/02/03追記 スライド63がちょっと正確でない気がしてきましたので、調査中です。近いうちに修正します。
参考書としては、こちらがわかりやすいです。
 オイラーの定理を導くまで
オイラーの定理を導くまで
[latexpage]
オイラーの定理は、法$m$としたときのオイラー関数$\phi (m)$、さらには$m$と互いに素な整数$a$を用いて、次のように表されます。
\begin{eqnarray}
a^{\phi (m)} \equiv 1 \bmod m
\end{eqnarray}
この定理は初等数論における非常に重要な定理として位置づけられています。
一見、オイラー関数が入っていていたりして、状況が分かりにくいですが、次の補助定理を認めてしまえば、非常に簡単に理解できるものです。
補助定理:
$\{a_1, a_2, \cdots , a_{\phi (m)}\}$ が $m$ を法とする既約剰余系で ${\gcd(c, m)=1}$ ならば,$\{ca_1, ca_2, \cdots , ca_{\phi (m)}\}$ も $m$ を法とする既約剰余系である.
この補助定理は、既約剰余系の要素$a_i$が法$m$と互いに素、すなわち、${\gcd(a_i, m)=1}$であることと、合同式の割り算、つまり、
$ac\equiv bc \bmod m$ ならば,$a \equiv b \bmod m/d$.ここで,$d=\gcd (c, m)$
から、容易に導くことが出来ます。よろしければやってみてください。(文献[1]の定理5.9下に証明が載っています。)
さて、ここで法$m$の既約剰余系を${\boldmath A}$とし、${\boldmath A}$の要素数を$|{\boldmath A}|$とすると、
\begin{eqnarray}
{\boldmath A}=\{a_1, a_2, \cdots , a_{|{\boldmath A}|}\}
\end{eqnarray}
また、${\boldmath A}$のすべての要素に対し、${\gcd(c, m)=1}$となる$c$を掛けて、既約剰余系${\boldmath A’}$を作る。
\begin{eqnarray}
{\boldmath A’}=\{ca_1, ca_2, \cdots , ca_{|{\boldmath A}|}\}
\end{eqnarray}
補助定理より、${\boldmath A}={\boldmath A’}$であるから、「${\boldmath A}$のすべての要素の積」と「${\boldmath A’}$のすべての要素の積」は等しい。
したがって、
\begin{eqnarray}
c^{|{\boldmath A}|} a_1a_2\cdots a_{A}\equiv a_1a_2\cdots a_{|{\boldmath A}|} \bmod m
\end{eqnarray}
ここで、既約剰余系の各元$a_i$は定義より法$m$と互いに素であるから、その元の積である$a_1a_2\cdots a_{|{\boldmath A}|}$も$m$と互いに素である。
したがって、両辺から$a_1a_2\cdots a_{|{\boldmath A}|}$を消去できて、
\begin{eqnarray}
c^{|{\boldmath A}|} \equiv 1 \bmod m
\end{eqnarray}
上記で$c$–>$a$と置き換えればオイラーの公式の完成ですね。ここで、法$m$における既約剰余系の要素数$|{\boldmath A}|$が、オイラー関数$\phi (m)$に一致することを思い出してください。
疑問:既約剰余系の要素数はオイラー関数?
ここで頭がごっちゃになっている人がいるかもしれませんので、いったん整理しましょう。
まず、オイラー関数の定義は、「$m$以下の$m$と互いに素な整数の数」、でした。そして、既約剰余系の定義は、「$m$以下の$m$と互いに素な整数の集合」、でした。よって、「法$m$における既約剰余系の要素数」はオイラー関数$\phi (m)$に等しくなるのは定義から明らかですね。
そして、「既約剰余系の要素は法$m$と互いに素である」、という事実から、補助定理を導き、その補助定理から、オイラーの定理を導きました。
以上が証明の流れです。
具体的な例を考えて、オイラーの定理の意味を考えてみましょう。
法を9として考えましょう($m=9$ですね)。
さて法9における、剰余類の集合は$\mathbb{Z}/9\mathbb{Z}=\left\{0, 1, 2, 3, 4, 5, 6, 7, 8\right\}$として表せます。
ここで法9における、既約剰余系は、9と互いに素な要素を抜き出したものですから、$\left(\mathbb{Z}/9\mathbb{Z}\right)^{\times}=\left\{1, 2, 4, 5, 7, 8\right\}$となります。
この中から、どれでもいいので1つ要素を取り出して(たとえば2を取り出して)それぞれの要素と積をとってみます。それぞれの要素に2をかけて得られた要素を集めた集合は、既約剰余類$\left(\mathbb{Z}/9\mathbb{Z}\right)^{\times}$に一致します。これが補助定理の意味することでした。
図に表すと以下のようになります。
さらに2をかけ続けていき、各要素の値の変化を追いかけると、$\left(\mathbb{Z}/9\mathbb{Z}\right)^{\times}$の場合は、ちょうどすべての要素を巡回するように値がかわっていきます。
そして、$\left(\mathbb{Z}/9\mathbb{Z}\right)^{\times}$の要素の数だけ積をとって巡回すると($\left(\mathbb{Z}/9\mathbb{Z}\right)^{\times}$の場合は6回)1になって、さらに1回積をとると元の値に戻ってくるのです。これがオイラーの定理の真の意味です。
ところで、$\left(\mathbb{Z}/9\mathbb{Z}\right)^{\times}$において、2は$\left(\mathbb{Z}/9\mathbb{Z}\right)^{\times}$の要素数だけかけないと元には戻りませんでした。
この例の2ように、$\left(\mathbb{Z}/m\mathbb{Z}\right)^{\times}$の要素数回だけ積をとって、初めて1になるような数を、「法mにおける原始根」といいます。(原始根が存在しないような法もあります。)
当然、それより前に1になるような数も出てくるわけです。単純に考えると、1は任意の法mにおいて、1回の積で1になりますね。このように、ある整数$a$が法$m$において、1になるために必要な積の回数を、法$m$における$a$の位数と呼びます。
実は、原始根や位数に関する一般的なことはあまりわかっていないそうなのです。なかなか奥が深くて面白いですね。
オイラーの定理が使いこなせると、べき乗の合同式の計算がとても速くなりますね。また、RSA暗号のような応用でも重要な要素として登場したりします。
それでは、今日はこの辺で。
参考文献:
[1] James J. Tattersall原著、「初等整数論9章 第2版」、森北出版株式会社
[2] ジョセフ・H・シルヴァーマン著、「はじめての数論 原著第3版」、ピアソン・エデュケーション
 繰り返し自乗法
繰り返し自乗法
[latexpage]
繰り返し自乗法とは、ある自然数$a$の$m$を法としたべき乗、つまり、
\begin{eqnarray}
a^k \bmod m
\end{eqnarray}
を高速に求める計算法です。
この計算は、べき乗数$k$が小さい場合は何ともありませんが、たとえば、
\begin{eqnarray}
13^{400} \bmod 31
\end{eqnarray}
のような場合は、単純にべき乗していくと値が指数爆発して簡単には求まりませんし、毎回積のmodをとっていくにしても計算量が多くなってしまいますね。この場合は法$m$が素数ですから、フェルマーの小定理によって計算が楽になりますし、そうでない場合も法$m$のオイラー関数$\phi (m)$が計算できれば、オイラーの定理が使えます。しかしながら、この考え方は、法$m$の素因数分解が出来ることが前提ですし、何より一般的ではありません。
指数のべき乗の余りなんて、どこで使うんだと思う方もいると思います。具体的な例として、RSA暗号が挙げられます。(参考:RSA暗号の数理 http://nsplat.wordpress.com/2012/02/12/)
暗号化と復号化は、まさにこの巨大数のべき乗です。
そこで本記事では、一般の法$m$に対して用いることが出来る繰り返し自乗法という方法を考えます。
繰り返し自乗法の手順は3ステップに分けられます。
1. 指数$k$を二進展開する
2. 指数の底$a$の自乗を計算し、これを繰り返し自乗していく
3. 1. で求めた二進数の{0, 1}に対応して、1のときだけ、2.の値を掛け合わせる
では、式(1)に関して計算してみましょう。
1. 指数$k$を二進展開する
$k$を二進展開します。
\begin{eqnarray}
k=u_0\cdot 2^0+u_1\cdot 2^1+u_2\cdot 2^2+\cdots
\end{eqnarray}
となります。
係数$u_i$は二進数に展開したときの第$i$位の値です。
これを指数の肩に載せてみましょう。
\begin{eqnarray}
a^k=a^{u_0\cdot 2^0+u_1\cdot 2^1+u_2\cdot 2^2+\cdots}
\end{eqnarray}
2. 指数の底$a$の自乗を計算し、これを繰り返し自乗していく
次に$a$を$A_0$とし、$A_0$の自乗$a^2$を$m$で割った余りを計算し、これを$A_1$とします。つまり
\begin{eqnarray}
a\equiv A_0 \bmod m
\end{eqnarray}
\begin{eqnarray}
\left(A_0\right)^2\equiv A_1 \bmod m
\end{eqnarray}
この得られた$A_1$をさらに自乗し、$m$で割った余りを$A_2$とします。これを繰り返し、$A_2, A_3, \cdots $としていきます。
\begin{eqnarray}
\left(A_1\right)^2\equiv A_2 \bmod m
\end{eqnarray}
\begin{eqnarray}
\left(A_2\right)^2\equiv A_3 \bmod m
\end{eqnarray}
この$A_i$は結局、$a^{2^i}$を$m$で割った余りに相当することがわかると思います。
すなわち、
\begin{eqnarray}
a^{2^i}\equiv A_i \bmod m
\end{eqnarray}
3. 1. で求めた二進数の{0, 1}に対応して、1のときだけ、2.の値を掛け合わせる
さて、式(4)を指数の性質から積に分解すると、
\begin{eqnarray}
a^k=a^{u_0\cdot 2^0}\cdot a^{u_1\cdot 2^1}\cdot a^{u_2\cdot 2^2}\cdot \cdots}
\end{eqnarray}
と表せます。
これを法$m$で考え、式(8)を適用すると、
\begin{eqnarray}
a^k&=&a^{u_0\cdot 2^0}\cdot a^{u_1\cdot 2^1}\cdot a^{u_2\cdot 2^2}\cdot \cdots\\
&\equiv& {A_0}^{u_0}\cdot {A_1}^{u_1}\cdot {A_2}^{u_2}\cdot \cdots\bmod m
\end{eqnarray}
したがって、二進展開した$k$の二進数における各位$u_i$が$1$に相当する$A_i$の積をとれば、求める指数が得られることがわかります。
これが高速であることを示すために、式(2)の値を具体的に計算してみましょう。
まず、400を二進展開します。
\begin{eqnarray}
400 = 0\times 2^0+0\times 2^1+0\times 2^2+0\times 2^3+1\times 2^4\\+0\times 2^5+0\times 2^6+1\times 2^7+1\times 2^8
\end{eqnarray}
次に、$13$の自乗を繰り返し計算します。
\begin{eqnarray}
\left(13^{2^0}\equiv \right)13 \equiv 13 \bmod 31\\
\left(13^{2^1}\equiv\right)13^2 \equiv 14 \bmod 31\\
\left(13^{2^2}\equiv\right)14^2 \equiv 10 \bmod 31\\
\left(13^{2^3}\equiv\right)10^2 \equiv 7 \bmod 31\\
\left(13^{2^4}\equiv\right)7^2 \equiv 18 \bmod 31\\
\left(13^{2^5}\equiv\right)18^2 \equiv 14 \bmod 31\\
\left(13^{2^6}\equiv\right)14^2 \equiv 10 \bmod 31\\
\left(13^{2^7}\equiv\right)10^2 \equiv 7 \bmod 31\\
\left(13^{2^8}\equiv\right)7^2 \equiv 18 \bmod 31\\
\end{eqnarray}
最後に、式(11)の指数に合わせて積をとると、
\begin{eqnarray}
13^{400} &=& 13^{0\times 2^0+0\times 2^1+0\times 2^2+0\times 2^3+1\times 2^4+0\times 2^5+0\times 2^6+1\times 2^7+1\times 2^8}\\
&\equiv & 13^0\cdot 14^0\cdot 10^0\cdot 7^0\cdot 18^1 \cdot 14^0 \cdot 10^0 \cdot 7^1 \cdot 18^1 \bmod 31\\
&\equiv & 18^1\cdot 7^1 \cdot 18^1 \bmod 31\\
&\equiv & 5 \bmod 31
\end{eqnarray}
となって計算できました。
どれぐらい簡単になったか、積の回数で比較しましょう。
普通に13を400回かけるとすると、積の回数は399回ですね。
一方、繰り返し自乗法では、13の自乗を繰り返し計算するフェーズ2.で8回、それらの積を計算するフェーズで2回の積、合計10回で済みます。
ずいぶんと計算が簡略化されましたね!
一般的に考えると、繰り返し自乗法では、指数$k$の二進展開の桁数を$d$すなわち、$\log_2 k = d$としたとき、その積の回数は$\mathcal{O}(d)$となることが知られています。べき乗をただ計算する計算法のオーダーが$\mathcal{O}(2^d)$となることを考えると、非常に効率的なアルゴリズムであることがわかるでしょう。
アルゴリズムの実装は多少難しいように思えるかもしれませんが、実は結構簡単です。
以下はJavaでの実装ですが、次のように、非常に簡潔に書くことが出来ます。
public static BigInteger power(BigInteger x, BigInteger k, BigInteger m){
BigInteger v = BigInteger.ONE;
if(k.equals(BigInteger.ZERO))
return v;
BigInteger p = x.remainder(m);
BigInteger two = BigInteger.ONE.add(BigInteger.ONE);
while(k.compareTo(BigInteger.ZERO) > 0){
if(k.remainder(two).equals(BigInteger.ONE))
v = (v.multiply(p)).remainder(m);
p = (p.multiply(p)).remainder(m);
k = k.shiftRight(1);
}
return v;
}
参考文献
[1] ジョセフ・H・シルヴァーマン著、鈴木治郎訳、はじめての数論、ピアソン・エデュケーション
 Moduloとお友達になろう
Moduloとお友達になろう
tsujimotterが参加している某勉強会で発表したスライドです。
3分プレゼン大会と題して、メンバー全員がそれぞれ1テーマの短いプレゼンを次々と発表しました。
テーマの縛りはなかったので、私は好きな数学のお話をしました。
普段から数学の話をしているのですが、ちょくちょくmoduloの話が出てきて、そのたびに説明に詰まって歯がゆい思いをしていたのでいっそ基礎の部分を説明してしまうか、と考えて作った発表です。
想いが熱すぎて3分を大きく超えてしまいましたが(実際7分程度話していました)、modulo計算について噛み砕いて説明したつもりです。
ここら辺の話が分かってくると、オイラーの公式とかフェルマーの小定理とか、中国の剰余定理とかわかってきて、RSA暗号とかのホットな応用も話せるのでたのしいのですよね。
実は、この分野を最初に体系化した人はガウスだったりして、なかなか興味深い。
[追記]
スライドでは応用例として「2012を9で割った余り」を紹介していますが、同じ要領で「2012を99で割った余り」も計算できます。簡単に計算できますので、ぜひチャレンジしてみてください。
 数学ガール読書会@札幌( #数学ガール札幌 )、立ち上げます
数学ガール読書会@札幌( #数学ガール札幌 )、立ち上げます
札幌を中心に、数学ガール(参考:『数学ガール』シリーズ http://www.hyuki.com/girl/)を片手に数学について語り合う読書会を立ち上げたいと思います。
数学ガール読書会@札幌
公式ハッシュタグ(予定) #数学ガール札幌
第0回予定 2012年10月ごろ
立ち上げの動機
数学および数学ガールが大好きな発起人(大学院生・札幌在住)が「みんなで数学ガールの話をして盛り上がれたら楽しそうだなあ」と妄想していたところ、どうやら仙台でそのようなイベントが立ち上がるとのこと。
数学ガール読書会仙台 第0回 http://atnd.org/events/32339
「仙台は遠いよー」「札幌でないかなー」などと呟いておりましたら、作者の結城さん(@hyuki)にリツイートして頂いたり、何人かの方に反応して頂きました。
皆さんのレスポンスに勇気を頂きまして、勝手ながら、札幌の数学ガール読書会を立ち上げようと考えた次第です。
想定している参加者
- 単純に数学ガール(数学)が好きで、数学ガール(数学)の魅力について語り合いたい
- 数学ガールを買ったはいいが、平積みしていて、これを機に読んでみたい
- 数学ガールをもう一度読み直して、わからなかったことを再度理解したい
- 数学ガールで取り上げた数学テーマ(FLT、ゲーデル、ガロア理論など)に興味がある
- 数学ガールは小説として大好き
- ミルカさまの大ファン
などなど、「数学ガールに興味があって、札幌在住の方なら誰でも可」、という感じで考えています。
発起人は、数学ガールをきっかけにガロア理論にはまってしまいまして、ガロア理論の専門書を大量に買ってしまいました。まだ、理解はし切れていないので、「アフター数学ガール的」な発展の部分も一緒に勉強し合えたらなあと考えています。
進め方
具体的な進め方は、プレゼン形式なのか、輪読なのか、とかはまだ何にも考えていませんが、「参加してみたいなー」って漫然と思っている方で集まって決めれたらなあと思います。
発起人としては、まずは最新刊のガロア理論あたりをテーマにできればなと思います。ひとまず2012年10月頃に第0回として集まってみませんか。
参加希望者、ご意見お待ちしています!
札幌近郊にお住まいの方で、参加ご希望の方いらっしゃいましたら、下記連絡先か、本記事のコメント欄にご連絡お願いします。
数学ガール勉強会@札幌 発起人 辻
twitter: @tsujimotter
e-mail: xxxxxxx (削除しました)
まだ、詳細はまったく決まっておりませんので、「こんな感じでやってほしい」「こういう場所でやりたい」など、ご意見大歓迎です!お気軽にご連絡ください。周りに数学ガール好きそうな人がいらっしゃいましたら、宣伝頂けるととても嬉しいです。宜しくお願いいたします!
2012/9/30追記:
読書会用のWikiページを立ち上げました。詳細はこちらに書き込んでいきますので、興味のある方はご確認を。
http://tsujimotter.info/mathgirl/pukiwiki/index.php?MathGirlTop
(スパムが多いので削除しました)
 logsumexp
logsumexp
[latexpage]
*
大きさが極端に小さい/大きい「重み」の値の和を求める際に、アンダーフロー/オーバーフローを防ぐための方法です。ベイズで周辺確率を求めるときなど計算機統計の分野でしばしば用いられます。
*
応用の幅は広いと思いますが、今回はパーティクルフィルタという手法を例にとり、説明します。
 鳩の巣原理
鳩の巣原理
[latexpage]
*
中学生でもわかりそうなのに、解法はなかなか思いつかない。簡単なのに奥が深い、そんな問題です。
*
問題
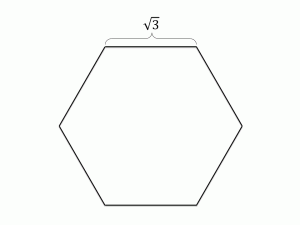
図1のような一辺が√3の正六角形の土地に19本の木を植えたいと思います。
ただし、この木は半径1以内に別の木が植えられていると、栄養が足りなくなり枯れてしまいます。
枯れさせることなく、この土地に19本の木を植えることができるでしょうか。
(できる場合は、その方法を。できない場合はその証明を考えてみてください。)
この問題は数学オリンピックの問題を私が若干改変したものです。(変えたのは辺の長さだけです。)
答えが分かった人は、続き↓をどうぞ。
 正十七角形の作図
正十七角形の作図
小学校や中学校で、定規とコンパスを使った作図を習うと思います。正多角形の作図も授業の中で習った記憶がありますが、せいぜい正三角形と正五角形くらいだったと思います。「正十七角形が作図可能である」と聞くと、少し驚きませんか。
歴史を振り返ると、ギリシャの時代から18世紀の後半まで、これ以外の正素数角形の作図法は知られていませんでしたし、作図できるとも思われていなかったようです。
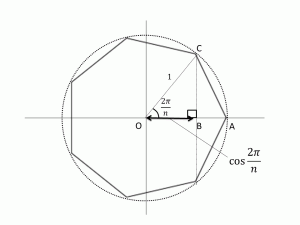
一般に、$n$を自然数としたとき、正$n$角形の作図は、単位円を書きその円周を$n$等分する点を作図する問題に帰着されます。さらにその等分点の作図は、次のような手順により$\cos \frac{2\pi}{n}$の作図に帰着できるのです。
中心Oで半径1の単位円を書き、Oを通る直線を引きます。この直線と円の交点をAとします。直線AO上にBO=$\cos\frac{2\pi}{n}$となる点Bをとります。点Bを通る直線AOに垂直な直線を引き、円との交点をCとします。単位円の弧ACが、単位円を$n$等分する弧となるので、コンパスでACの長さをとって、次々と等分点を作っていきます。これで正$n$角形のすべての頂点の作図が完成です。
 ベルヌーイ数 (4): ベルヌーイ数を求めるアルゴリズム
ベルヌーイ数 (4): ベルヌーイ数を求めるアルゴリズム
[latexpage]
ベルヌーイ数の定義は以下のように与えられました。
\[
\begin{eqnarray}
\sum_{j=0}^{k} \binom{k+1}{j} b_j &=& k+1 \tag{1}\\
b_0 &=& 1 \tag{2}
\end{eqnarray}
\]
今回は、この数列の簡便な計算方法を紹介しましょう。