 鳩の巣原理
鳩の巣原理
[latexpage]
*
中学生でもわかりそうなのに、解法はなかなか思いつかない。簡単なのに奥が深い、そんな問題です。
*
問題
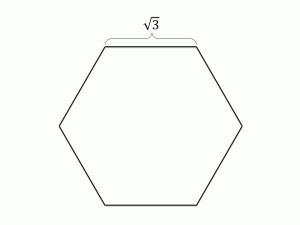
図1のような一辺が√3の正六角形の土地に19本の木を植えたいと思います。
ただし、この木は半径1以内に別の木が植えられていると、栄養が足りなくなり枯れてしまいます。
枯れさせることなく、この土地に19本の木を植えることができるでしょうか。
(できる場合は、その方法を。できない場合はその証明を考えてみてください。)
この問題は数学オリンピックの問題を私が若干改変したものです。(変えたのは辺の長さだけです。)
答えが分かった人は、続き↓をどうぞ。
*
*
*
*
*
解答・解説
当然(?)ですが、答えは「できない」です。
*
証明の前に、簡単に考え方を整理してみましょう。
*
キーとなる考え方は、本記事の表題にもある「鳩の巣原理」です。鳩の巣原理は、別名「ディリクレの箱入れ原理」とも呼ばれています。ディリクレが1834年に書いた論文に起源があるそうです。その内容は、小学生でも理解できそうなシンプルなものです。
(実際、『ハトと「ハトの巣」』というタイトルの児童書も出ています。私も持っていますが、鳩の巣原理を小学生にもわかるように解説した本です。具体例がたくさん載っていて大人でも読める本です。amazonへのリンク。)
*
*
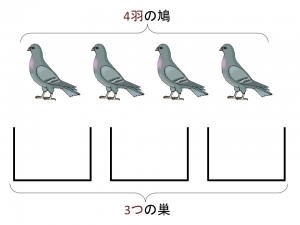
図2のように、$n$つの巣に対し、1だけ多い$(n+1)$羽の鳩がいるとします。
(図では$n=3$、3つの巣と4羽の鳩としています。)
ここで$(n+1)$羽のすべての鳩をいずれかの巣の中に戻します。
このとき、巣に入らない鳩はいないものとします。
*
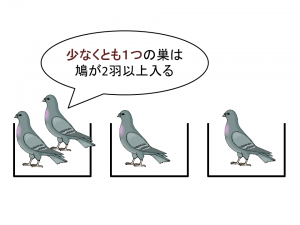
すると、巣に戻った鳩のパターンは、たとえば図3のようになるでしょう。
図3では、一番左の巣には2羽以上の鳩が入っていることがわかります。
*
重要なことは、たとえ「どんなパターンで鳩が入ったとしても、少なくとも1つの巣には鳩が2羽以上入る」ということです。このことは、鳩の巣原理と呼ばれています。
*
鳩の巣原理を言い換えると次のように表現できます。
鳩の巣原理:
$m$個の元からなる集合$A$から、$n$個の元からなる集合$B$への写像$f$を考えたとき、$m>n$ならば$f$は単射ではない
$f$が単射であるとは、$B$のある元に対する逆像が高々1個ということです。
これは、いずれの鳩の巣も、入っている鳩の数は0羽か1羽であることに相当します。
単射ではないので、2羽以上入る巣が存在するということですね。
*
*
さて、ではこの鳩の巣原理をどのように使えばよいでしょうか。
*
問題を簡単にして考えてみましょう。
*
土地の形を正方形にして、一辺の長さを1とします。植える木の本数は5本です。
ここで図4のように土地を4分割して、5本の木を植えていきます。
*
気づいたでしょうか。
そう、鳩の巣原理を使いたいのです。
*
この場合、分割した4つの領域が巣に、5本の木が鳩に相当します。
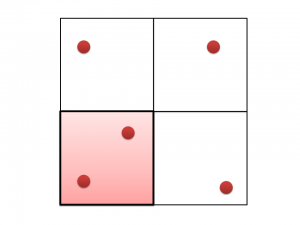
5本の木を植えてみるとたとえば図5のようになるでしょう。
(木の植えた場所は赤丸で表現しています。)
鳩の巣原理により、少なくとも1つの領域には、2本以上の木が入ることになります。
図では左下の1領域に2本入っていますが、このようなことはいずれのパターンでも起きます。
*
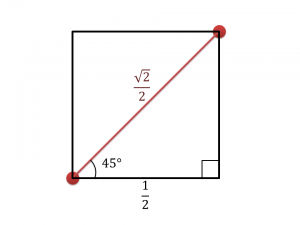
この2本の木が入った領域の中で、最大限距離をとって木を置いてみます。
領域は正方形ですから、距離が最大となるのは図6のように対角に置いた場合です。
この場合、対角の長さは$\frac{\sqrt{2}}{2}$なります。
したがって、同じ領域に入った2本の木はどこに置いたとしても、距離は$\frac{\sqrt{2}}{2}$以下となることがわかります。
*
ここで、鳩の巣原理から、少なくとも2本は同じ領域にあるわけですから、「少なくとも2本は距離が$\frac{\sqrt{2}}{2}$以下である」ということが証明できました。
つまり、一辺の長さ1の正方形の土地に、それぞれの距離を$\frac{\sqrt{2}}{2}$より離して、5本以上の木を植えることができないということです。
*
2本以上入った領域以外の土地に対しては、このように実際の置き方を一切考えることなく証明できてしまいました。
これが鳩の巣原理の面白い所です。
*
*
同じような考え方で、最初の問題を考えてみましょう。
*
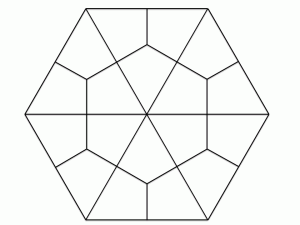
今度の木は19本なので、正六角形を18分割することにします。
分割の仕方は多少技巧的ですが、図7のように分割すればよいことがわかります。
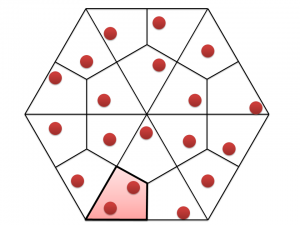
ここに19本の木を植えていきます。たとえば、図8のように。
図8では左下の凧形の領域に2本の木が入っていますが、鳩の巣原理によると、少なくとも1つの領域には2本以上の木が入ります。
この2本の木の間隔が最大でも$1$までしか広げられないことが示せれば、証明完了です。
*
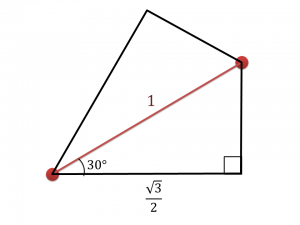
この凧形の領域の中で距離が最大となるのは、図9のように対角に置いた場合です。
図の通り、求める長さは一つの鋭角が30°となる直角三角形の斜辺となります。
$1:2:\sqrt{3}$より、斜辺の長さは$1$です。
*
これにより、「19本の木のうち少なくとも2本は距離が$1$以下である」ということが証明できました。
最初の問いに戻ると、すべての木が枯れることなく19本の木を植えることはできません。
*
*
いかがでしたか。
*
証明に使った道具は、鳩の巣原理と直角三角形の辺の比だけでした。辺の比は、いわゆる三角定規の簡単な辺の比でしたし、鳩の巣原理自体もとてもシンプルなものです。
鳩の巣原理を適用しようというのは、なかなか思いつかないかもしれませんが、知っているといろいろな問題に適用できます。
鳩の巣原理は高校でも習いません。当たり前のことを表現しているだけのように思えるかもしれません。
しかしながら、具体的な方法を考えることなく重複の存在を証明できてしまう、マジックのような趣きを持った興味深い証明方法です。これぞ数学という手法ではないでしょうか。
適切な問題で使うことが出来れば、気持ちいいこと間違いありません。
*
検索エンジンで鳩の巣原理と調べてみるとたくさん例が出てきますので、ぜひ調べてみてください。有名なものだと格子点の問題があります。
*
私のおすすめは下記のサイトです。たくさんの応用が出ていて面白いです。
http://www004.upp.so-net.ne.jp/s_honma/pigeon/pigeon.htm
*
*
長くなりましたが、今日はこの辺で。
*
*
追記:
実はこの問題に私が出会ったのは、コマネチ大学数学科というテレビ番組でした。
このほかにも面白い問題が紹介されていて筆者が大好きな番組の一つです。
番組で紹介された問題は下記のブログでも紹介されていますので、ぜひ見てみてください。
http://gascon.cocolog-nifty.com/blog/2010/08/190-2ee0.html

Good I should certainly pronounce, impressed with your website. I had no trouble navigating through all the tabs as well as related info ended up being truly simple to do to access. I recently found what I hoped for before you know it at all. Reasonably unusual. Is likely to appreciate it for those who add forums or something, web site theme . a tones way for your customer to communicate. Excellent task..
This is both street smart and itnellignet.
This is crystal clear. Thanks for tankig the time!
That’s an ingenious way of thinnikg about it.