小学校や中学校で、定規とコンパスを使った作図を習うと思います。正多角形の作図も授業の中で習った記憶がありますが、せいぜい正三角形と正五角形くらいだったと思います。「正十七角形が作図可能である」と聞くと、少し驚きませんか。

歴史を振り返ると、ギリシャの時代から18世紀の後半まで、これ以外の正素数角形の作図法は知られていませんでしたし、作図できるとも思われていなかったようです。

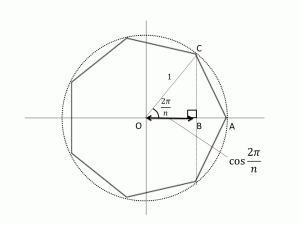
一般に、$n$を自然数としたとき、正$n$角形の作図は、単位円を書きその円周を$n$等分する点を作図する問題に帰着されます。さらにその等分点の作図は、次のような手順により$\cos \frac{2\pi}{n}$の作図に帰着できるのです。

中心Oで半径1の単位円を書き、Oを通る直線を引きます。この直線と円の交点をAとします。直線AO上にBO=$\cos\frac{2\pi}{n}$となる点Bをとります。点Bを通る直線AOに垂直な直線を引き、円との交点をCとします。単位円の弧ACが、単位円を$n$等分する弧となるので、コンパスでACの長さをとって、次々と等分点を作っていきます。これで正$n$角形のすべての頂点の作図が完成です。

作図とガウス

ところで、正十七角形の作図可能性を示したのは、あの有名なガウスです。

ガウスが19歳のころ、下記の式を導いて、正十七角形が作図可能であることを示しました。

\[
\begin{eqnarray}
\cos\frac{2\pi}{17} = -\frac{1}{16}+\frac{\sqrt{17}}{16}+\frac{\sqrt{2\left(17-\sqrt{17}\right)}}{16} + \frac{\sqrt{17+3\sqrt{17}-\sqrt{2\left(17-\sqrt{17}\right)}-2\sqrt{2\left(17+\sqrt{17}\right)}}}{8}
\end{eqnarray}
\]

この式から、「$\cos\frac{2\pi}{17}$が四則演算とルートのみを使って構成される」ことが一目でわかります。これは「$\cos\frac{2\pi}{17}$が作図可能である」ことの必要十分条件となっています。

ガウスがこの式を思いついたのは、目覚めの瞬間であったという逸話もあります。真偽はともかく、ギリシャ時代からガウスの発見まで2000年近くに渡って、正三角形、正五角形以外の正素数角形は作図不能だと思われていたそうですから、この結果は衝撃的なものであったでしょう。この結果の発見がきっかけで、ガウスが数学者を志したというエピソードも知られていますが、それも十分に納得出来る理由となっています。

ガウスはこの後、これらの結果を円分体の理論として体系化し、自身の著書「整数論の研究（原題: Disquisitiones Arithmeticae）」の第七章で論じています。その中で、正十七角形のみならず、一般の正多角形に対しても、定規とコンパスによって作図できる条件を与えています。

さて、ガウスはどのような考えでこのような結果を導いたのでしょうか。そして、正十七角形はどのような手順で作図できるのでしょう。この記事では正十七角形の作図手順と共に、その作図に必要な$\cos \frac{2\pi}{17}$が定規とコンパスを使って得られることを示したいと思います。

作図手順

まず、Oを中心とする単位円を書きます。

Oを通る直線とその直線の垂線を引き、最初の直線と円の交点をA、垂線と円の交点をBとします。

次に、OAを1:3で内分する点をCとします。これは、線分OAの垂直二等分線を作図して中点をC’とし、OC’をさらに二等分する中点をCとすれば作図できるでしょう。

このとき$OB=1$、$OC=\frac{OA}{4}=\frac{1}{4}$であるから、直角三角形OBCにピタゴラスの定理を適用して、

\[
\begin{eqnarray}
BC^2&=&OB^2+OC^2\\
&=&1^2+\left(\frac{1}{4}\right)^2=\frac{17}{16}\\
\therefore BC&=&\frac{\sqrt{17}}{4}
\end{eqnarray}
\]

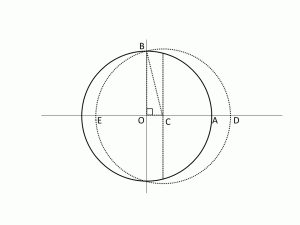
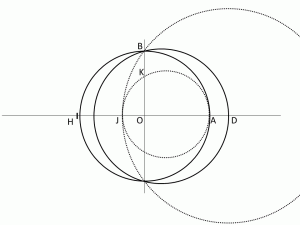
さらに、コンパスでBCの長さをとって、Cを中心に円を書き、直線OAとの交点D, Eを図のように取ります。

ここで、OD, OEは次のように得られます。

\[
\begin{eqnarray}
OD&=&OC+BC=\frac{1+\sqrt{17}}{4}\\
OE&=&-OC+BC=\frac{-1+\sqrt{17}}{4}
\end{eqnarray}
\]

ここで、BEは直角三角形OBEの辺であるから、ピタゴラスの定理より、

\[
\begin{eqnarray}
BE^2&=&OB^2+OE^2\\
&=&1^2+\left(\frac{-1+\sqrt{17}}{4}\right)^2=\frac{34-2\sqrt{17}}{16}\\
\therefore BE&=&\frac{\sqrt{34-2\sqrt{17}}}{4}
\end{eqnarray}
\]

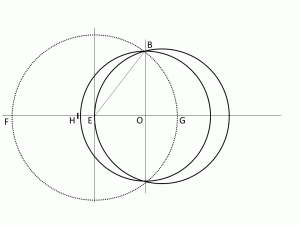
BEを中心に円を書き、図のように直線OAとの交点F, Gをととります。

\begin{eqnarray}
OF&=&OE+BE=\frac{-1+\sqrt{17}}{4}+\frac{\sqrt{34-2\sqrt{17}}}{4}\\
OG&=&-OE+BE=-\frac{-1+\sqrt{17}}{4}+\frac{\sqrt{34-2\sqrt{17}}}{4}
\end{eqnarray}

さらに、OFの中点Hをとります。

その長さOHを定数$a$とします。

\[
\begin{eqnarray}
OH=\frac{OF}{2}=\frac{-1+\sqrt{17}}{8}+\frac{\sqrt{34-2\sqrt{17}}}{8}=a
\end{eqnarray}
\]

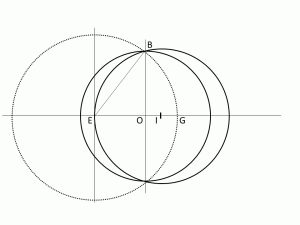
ここで、OGの中点Iをとり、OIの長さを$-b$とします。

\[
\begin{eqnarray}
OI=\frac{OG}{2}=-\frac{-1+\sqrt{17}}{8}+\frac{\sqrt{34-2\sqrt{17}}}{8}=-b
\end{eqnarray}
\]

この変数$b$は作図では使いませんが計算上後で使うことになります。

次にBDの長さをコンパスでとり、Dを中心に円を描きます。円と直線OAの交点を図のようにJとします。

ここで、直角三角形OBDにピタゴラスの定理を適用して、

\[
\begin{eqnarray}
BD^2&=&OB^2+OD^2\\
&=&1^2+\left(\frac{1+\sqrt{17}}{4}\right)^2=\frac{34+2\sqrt{17}}{16}\\
\therefore BD&=&\frac{\sqrt{34+2\sqrt{17}}}{4}
\end{eqnarray}
\]

よってOJは、
\[
\begin{eqnarray}
OJ=-OD+BD=-\frac{1+\sqrt{17}}{4}+\frac{\sqrt{34+2\sqrt{17}}}{4}
\end{eqnarray}
\]

OJを$2c$とおくと下式で表されます。（この変数も作図では用いません。）
\[
\begin{eqnarray}
c=\frac{OJ}{2}=-\frac{1+\sqrt{17}}{8}+\frac{\sqrt{34+2\sqrt{17}}}{8}
\end{eqnarray}
\]

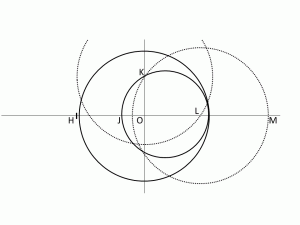
AJを直径とする円を描き、直線OBとの交点を図のようにKとします。

ここでKはAJを直径とする円周角より、$\angle{AKJ}=90^{\circ}$。また$\angle{KOJ}=90^{\circ}$、$\angle{AOK}=90^{\circ}$であるから、$\triangle {KOJ} \sim \triangle {AOK}$。したがって、
\[
\begin{eqnarray}
\frac{OK}{OJ}&=&\frac{OA}{OK}\\
\therefore \frac{OK}{2c}&=&\frac{1}{OK}\\
\therefore OK^2&=&2c\\
\therefore OK&=&\sqrt{2c}=\sqrt{-\frac{1+\sqrt{17}}{4}+\frac{\sqrt{34+2\sqrt{17}}}{4}}
\end{eqnarray}
\]

コンパスでOHの長さをとり、Kを中心に円を描く。その円と直線OAの交点Lを図のようにとる。

さらに、KLの長さをとり、Lを中心に円を描き、円と直線OAの交点Mを図のようにとる。

ここで手順より、
\[
\begin{eqnarray}
OH=KL=LM=a
\end{eqnarray}
\]
であり、$\triangle {KOL}$は直角三角形であるから、
\[
\begin{eqnarray}
OM&=&LM+OL\\
&=&LM+\sqrt{KL^2-OK^2}\\
&=&a+\sqrt{a^2-2c}
\end{eqnarray}
\]

ここで公式、
\[
\begin{eqnarray}
2a^2=2+b+2c
\end{eqnarray}
\]

を認めると、
\[
\begin{eqnarray}
\therefore a^2-2c=1+\frac{b}{2}-c
\end{eqnarray}
\]

より、
\[
\begin{eqnarray}
OM&=&a+\sqrt{a^2-2c}\\
&=&a+\sqrt{1+\frac{b}{2}-c}\\
&=&\frac{-1+\sqrt{17}}{8}+\frac{\sqrt{34-2\sqrt{17}}}{8}\\
&&+\sqrt{1+\frac{-1+\sqrt{17}}{16}-\frac{\sqrt{34-2\sqrt{17}}}{16}+\frac{1+\sqrt{17}}{8}-\frac{\sqrt{34+2\sqrt{17}}}{8}}\\
&=&\frac{-1+\sqrt{17}}{8}+\frac{\sqrt{34-2\sqrt{17}}}{8}\\
&&+\sqrt{\frac{17+3\sqrt{17}-\sqrt{34-2\sqrt{17}}-2\sqrt{34+2\sqrt{17}}}{16}}\\
&=&\frac{-1+\sqrt{17}}{8}+\frac{\sqrt{34-2\sqrt{17}}}{8}\\
&&+\frac{\sqrt{17+3\sqrt{17}-\sqrt{34-2\sqrt{17}}-2\sqrt{34+2\sqrt{17}}}}{4}
\end{eqnarray}
\]

さあ仕上げです。

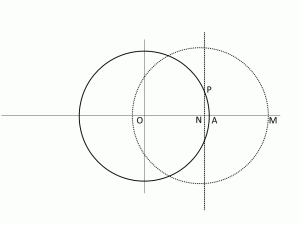
OMの中点Nをとる。

Nを通るOMの垂線（OMの垂直二等分線）を描き、円Oとの交点をPとする。

弧APは円Oの円周を17等分する弧となるから、この長さをとり繰り返し用いて正十七角形の頂点を作図する。（完成！）

NはOMの中点より、
\[
\begin{eqnarray}
ON&=&\frac{OM}{2}\\
&=&\frac{-1+\sqrt{17}}{16}+\frac{\sqrt{34-2\sqrt{17}}}{16}\\
&+&\frac{\sqrt{17+3\sqrt{17}-\sqrt{34-2\sqrt{17}}-2\sqrt{34+2\sqrt{17}}}}{8}
\end{eqnarray}
\]

これは(1)式の右辺に等しい！したがって、
\[
\begin{eqnarray}
ON=\cos\frac{2\pi}{17}
\end{eqnarray}
\]

これで$\cos\frac{2\pi}{17}$が作図できましたので、正十七角形の作図法の完成です。

しかしながら、式(1), (14)の正当性に関しては、まだ何も言っていませんね。

これについては、$\cos\frac{2\pi}{17}$の導出の際に説明することにしましょう。

補足

※ひとまず上記の問題に関しては、下記の記事の紹介で代用することにします。下記の記事中の変数a, b, cが本記事のa, b, cとそれぞれ対応しており、式(14)に対応する式も導出されています。

http://www.geocities.jp/phaosetc/misc/math/drawing/heptadecagon.html
↑久しぶりに開いてみたら、Yahoo!ジオシティーズの終了に伴い、上記の記事もウェブ上から削除されてしまっていたらしいのです。貴重なブログが……。Internet Archiveを探したら奇跡的に残っていたので、そちらのURLを再掲します。（2020/06/29追記）
https://web.archive.org/web/20181105204830/http://www.geocities.jp/phaosetc/misc/math/drawing/heptadecagon.html

関連記事

こちらの記事もどうぞ。
正十七角形は作れる – tsujimotter のノートブック