Archive for 7月, 2012
logsumexp
7月 27th, 2012 | 
Author: [latexpage]
＊
大きさが極端に小さい／大きい「重み」の値の和を求める際に、アンダーフロー／オーバーフローを防ぐための方法です。ベイズで周辺確率を求めるときなど計算機統計の分野でしばしば用いられます。
＊
応用の幅は広いと思いますが、今回はパーティクルフィルタという手法を例にとり、説明します。
Posted in 
鳩の巣原理
[latexpage]
＊
中学生でもわかりそうなのに、解法はなかなか思いつかない。簡単なのに奥が深い、そんな問題です。
＊
問題
図1: 正六角形の土地
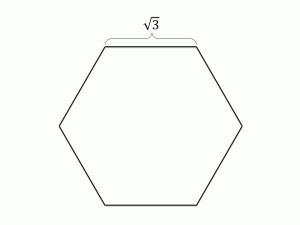
図1のような一辺が√3の正六角形の土地に19本の木を植えたいと思います。
ただし、この木は半径1以内に別の木が植えられていると、栄養が足りなくなり枯れてしまいます。
枯れさせることなく、この土地に19本の木を植えることができるでしょうか。
（できる場合は、その方法を。できない場合はその証明を考えてみてください。）
この問題は数学オリンピックの問題を私が若干改変したものです。（変えたのは辺の長さだけです。）
答えが分かった人は、続き↓をどうぞ。
正十七角形の作図
小学校や中学校で、定規とコンパスを使った作図を習うと思います。正多角形の作図も授業の中で習った記憶がありますが、せいぜい正三角形と正五角形くらいだったと思います。「正十七角形が作図可能である」と聞くと、少し驚きませんか。
歴史を振り返ると、ギリシャの時代から18世紀の後半まで、これ以外の正素数角形の作図法は知られていませんでしたし、作図できるとも思われていなかったようです。
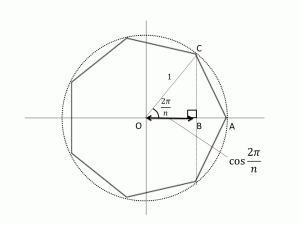
一般に、$n$を自然数としたとき、正$n$角形の作図は、単位円を書きその円周を$n$等分する点を作図する問題に帰着されます。さらにその等分点の作図は、次のような手順により$\cos \frac{2\pi}{n}$の作図に帰着できるのです。
図：cos(2π/n) 作図の流れ
中心Oで半径1の単位円を書き、Oを通る直線を引きます。この直線と円の交点をAとします。直線AO上にBO=$\cos\frac{2\pi}{n}$となる点Bをとります。点Bを通る直線AOに垂直な直線を引き、円との交点をCとします。単位円の弧ACが、単位円を$n$等分する弧となるので、コンパスでACの長さをとって、次々と等分点を作っていきます。これで正$n$角形のすべての頂点の作図が完成です。