tsujimotter

[latexpage]

前回：ベルヌーイ数 (3): ベルヌーイ数の正体

ベルヌーイ数の定義は以下のように与えられました。
\[
\begin{eqnarray}
\sum_{j=0}^{k} \binom{k+1}{j} b_j &=& k+1 \tag{1}\\
b_0 &=& 1 \tag{2}
\end{eqnarray}
\]

今回は、この数列の簡便な計算方法を紹介しましょう。

ここで、
\[
\begin{eqnarray}
\sum_{j=0}^{k+1} \binom{k+1}{j} b_j – b_k &=& k+1 \tag{3}\\
b_0 &=& 1 \tag{4}
\end{eqnarray}
\]

と変形すると、式の左辺第一項が下記の二項定理にそっくりに見えることがわかります。
\[
\begin{equation}
(1+b)^{k+1}=\sum_{j=0}^{k+1} \binom{k+1}{j} b^j \tag{5}
\end{equation}
\]

このことを利用して形式的に
\[
\begin{equation}
(1+b)^{k+1}\equiv \sum_{j=0}^{k+1} \binom{k+1}{j} b_j \tag{6}
\end{equation}
\]

とする表記法があります。これを用いれば、ベルヌーイ数の定義は以下のように簡潔に書くことが出来ます。
\[
\begin{eqnarray}
(1+b)^{k+1}-b^{k+1} &=& k+1 \tag{7}\\
b_0 &=& 1 \tag{8}
\end{eqnarray}
\]

このように、ベルヌーイ数は二項定理に深く関係する数列です。

そこで、二項係数のアナロジーで、「パスカルの三角形」のようなアルゴリズムが存在するのではないか、というアイディアが出て来るわけです。実際その直感は当たっています。

そのアルゴリズムを考えるために、ベルヌーイ数$b_k$の補助関数として$b_{k, m}$を定義します。$k, m$は次の範囲を動きます$k\geq 0, m\geq 1$。
\[
\begin{eqnarray}
b_{k+1, m} &=& m\left(b_{k, m}-b_{k, m+1}\right) \tag{9}\\
b_{0, m} &=& \frac{1}{m} \tag{10}
\end{eqnarray}
\]

この補助関数とベルヌーイ数との関係は、次のように表されます。
\[
\begin{equation}
b_k=b_{k, 1} \tag{11}
\end{equation}
\]

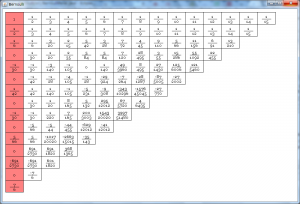
この方式は、パスカルの要領で、kを行、mを列として考えて、次の図のようにまとめることができます。

式の意味を考えると、隣り合う列の値の差をとり、その答えに列番号$m$をかけて得られた値を、左下に記述していけばよいことがわかります。

パスカルの三角形ほど計算は容易ではありませんが、一番左の列には確かにベルヌーイ数が並んでいます。

どうしてこのようなアルゴリズムになるのかは、

スターリング数と呼ばれる数列との関係を考えれば理解できるのですが、それはまたの機会にしましょう。

最後に、今回の図はJavaプログラムで作ったものです。

ソースコードをここにおいておきますので、（コードは汚いですが）よければ使ってみてください。（Bernoulli.javaのような名前で保存し、コンパイルすれば実行できるはずです。）

Bernoulli.java