 次元の呪い!?(1): 球面集中現象
次元の呪い!?(1): 球面集中現象
今日は1つの数学の問題について考えてみましょう。
We have a $\mathbb{R}^p$ unit ball which $N$ sampled uniformly.
1) Find the closest point to ${\bf 0}$. Let the distance be $r_{NN}$.
2) Repeat this with new $N$ samples.
3) Prove about the median $r^*$ of $r_{NN}$
\[
\begin{equation}
r^*=\left\{1-\left(\frac{1}{2}\right)^\frac{1}{N} \right\}^\frac{1}{p} \tag{1}
\end{equation}
\]
$p$次元球というのがまた考えにくいのですが、まずは $p=3$ あたりで考えてみてください。
1つの試行で半径 1 の 3 次元単位球の中に一様に点を押し込みます。それらの点と球の原点との距離 $r$ を考えるわけです。もっとも原点に近い点を Nearest Neighbor としてその距離を特別に $r_{NN}$ と名づけます。
この試行を繰り返した時の、$r_{NN}$ の分布の中央値 $r^*$ を求めよという問題です。
直観的には $r^*$ は原点付近に集まりそうですね。
この問題の結論は意外な結果になるのですが、このことが数学のみならず機械学習の分野に大きな哲学的な問いを呼び起こします。こちらについてはいつか別の記事で説明することにしましょう。
Nearest Neighbor $r_{NN}$ の数学的な扱い方がポイントになります。では行きましょう。
(解答)
$p$ 次元空間上でサンプリングした $N$ 点の内、Nearest Neighborとなる点が存在して、その点の原点からの距離 $r_{NN}$ が $r≤r_{NN}<r+{\mathrm d}r$ である確率を、確率密度関数 $f(r)$ を用いて、$f(r){\mathrm d}r$ と表すと、求める中央値は、
\[
\begin{equation}
\int_{r^*}^{1} f(r){\mathrm d}r=\frac{1}{2} \tag{2}
\end{equation}
\]
を満たす $r^*$ であることがわかる。
以下で、上述の議論に必要な確率密度関数 $f(r)$ を求め、中央値を導出する。
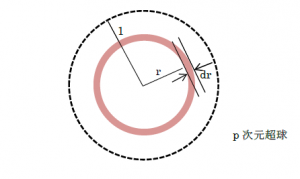
ここで半径 $r$ の $p$ 次元超球を考え、その体積を $V(r)$ とする
任意のサンプル点が、半径 $1$ の $p$ 次元超球に一様にばら撒かれたとき、あるサンプル $1$ 点が $[r, r+{\mathrm d}r]$ の球殻に入る確率は、入る領域の体積比で表されるため、
\[
\begin{equation}
\frac{V(r+{\mathrm d}r)-V(r)}{V(1)} \tag{3}
\end{equation}
\]
で表される。半径 $r$ の $p$ 次元球の体積は、$r$ の $p$ 乗に比例するため
$V(r)=cr^p$ とおくと、
\[
\begin{equation}
\frac{V(r+{\mathrm d}r)-V(r)}{V(1)} =\frac{c(r+{\mathrm d}r)^p-cr^p}{c}=pr^{p-1} {\mathrm d}r \tag{4}
\end{equation}
\]
となる。
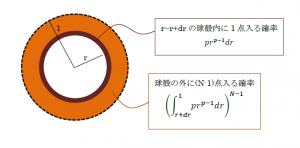
ここで題意より、上記の球殻に 1 点入って、残りの $N-1$ 点が球殻の外に入る場合の確率を求めればよいから、
\[
\begin{equation}
pr^{p-1} {\mathrm d}r\cdot \left(\int_{r+{\mathrm d}r}^1 pr’^{p-1} {\mathrm d}r’\right)^{N-1} \tag{5}
\end{equation}
\]
という確率分布を考えればよい。ただし、Nearest Neighbor に選ばれた $1$ 点は、$N$ 点のいずれでもよいため、$N$ を乗算して、
\[
\begin{equation}
f(r){\mathrm d}r=N\cdot pr^{p-1} {\mathrm d}r\cdot \left(\int_{r+{\mathrm d}r}^1 pr’^{p-1} {\mathrm d}r’\right)^{N-1} \tag{6}
\end{equation}
\]
が求める確率分布となる。
計算すると、
\[
\begin{eqnarray}
f(r){\mathrm d}r=N\cdot pr^{p-1} {\mathrm d}r\cdot \left(\int_{r+{\mathrm d}r}^1 pr’^{p-1} {\mathrm d}r’\right)^{N-1}\\
=N\cdot pr^{p-1} {\mathrm d}r\cdot \left([r’^p]_r^1 \right)^{N-1}=Npr^{p-1} (1-r^p )^{N-1} {\mathrm d}r \tag{7}
\end{eqnarray}
\]
ここで、求める中央値は、
\[
\begin{equation}
\int_{r^*}^{1} f(r){\mathrm d}r=\frac{1}{2} \tag{8}
\end{equation}
\]
となる $r^*$ にほかならないから、求めた $f(r)$ を代入して、
\[
\begin{equation}
\int_{r^*}^1 Npr^{p-1} (1-r^p )^{N-1} {\mathrm d}r=\frac{1}{2} \tag{9}
\end{equation}
\]
ここで、
\[
\begin{equation}
\frac{{\mathrm d}}{{\mathrm d}r} \left\{(1-r^p)^N \right\}=-Npr^{p-1} (1-r^p )^{N-1} {\mathrm d}r \tag{10}
\end{equation}
\]
であるから、上記の積分はただちに実行できて、
\[
\begin{equation}
\int_{r^*}^1 Npr^{p-1} (1-r^p )^{N-1} {\mathrm d}r=\left[-(1-r^p)^N\right]_{r^*}^1=\left(1-{r^*}^p \right)^N \tag{11}
\end{equation}
\]
\[
\begin{equation}
\therefore \left(1-{r^*}^p \right)^N=\frac{1}{2} \tag{12}
\end{equation}
\]
\[
\begin{equation}
\therefore r^*=\left\{1-\left(\frac{1}{2}\right)^{\frac{1}{N}} \right\}^{\frac{1}{p}} \tag{13}
\end{equation}
\]
となり、題意は証明された。
(証明終わり)
さて、結果はどうだったでしょうか。
\[
\begin{equation}
r^*=\left\{1-\left(\frac{1}{2}\right)^{\frac{1}{N}} \right\}^{\frac{1}{p}}\tag{14}
\end{equation}
\]
の$p$を大きくとると、$r^*$ は 1 に限りなく近づきます。
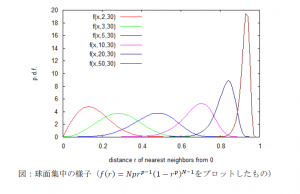
一様に点をとったはずなのに、点がほとんど球面に張り付いているように見えます。これを球面集中現象と言います。
確率密度関数 $f(r)$ をプロットしてみると、もっとわかりやすいかもしれません。$p$ が大きくなるにつれて、NN が 1 に張り付いていく様子が見てとれます。
Your post capeutrs the issue perfectly!
Kewl you should come up with that. Exlcenlet!
I adore this weblog, wonderful content material and I am going to bookmark this internet site for future updates.
こんにちは、またブログ覗かせていただきました。また、遊びに来ま~す。よろしくお願いします
With everything which seems to be building inside this area, many of your viewpoints tend to be somewhat stimulating. In any event I did enjoy reading it.
素晴らしい。勉強になりました。